12.7 Área bajo una curva
Como ya sabíamos, una de las aplicaciones de la integral definida es el cálculo de áreas. Profundicemos aún más en esta relación, combinándolo con el teorema de Barrow.
Función positiva
Si una función f(x) es continua y positiva en un intervalo [a, b], es decir, su gráfica se encuentra por encima del eje de abscisas, entonces el área de la región limitada por f(x), x = a y x = b está definida por:
Función negativa
Si una función f(x) es continua y negativa en un intervalo [a, b], es decir, su gráfica se encuentra por debajo del eje de abscisas, entonces el área de la región limitada por f(x), x = a y x = b está definida por:
Las integrales definidas de funciones negativas siempre dan un valor menor que cero. Por eso, a la hora de interpretar el resultado debemos cambiarle el signo, ya que no tienen sentido áreas negativas. Ése es el motivo por el que la integral definida va precedida del signo "menos" o dentro de un valor absoluto en funciones negativas.
Función positiva y negativa
Si una función f(x) es continua y cambia de signo en un intervalo [a, b], existiría un conflicto en cuanto al signo de la integral. Una posibilidad que se podría plantear es hallar el valor absoluto, de forma que siempre sea positivo. Sin embargo, esa solución sería incorrecta.
Veamos un ejemplo para entenderlo.
Queremos hallar el área de la función f(x) = x - 1 en el intervalo [0,2]. Si intentamos aplicar la fórmula anterior obtenemos:
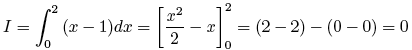
Ahora, procedamos de otra forma. Dividiremos el intervalo en [0,1] y [1,2] de forma que en cada uno la función no cambia de signo. Aplicamos así la fórmula adecuada en cada caso:
Comprobemos ahora que esta solución sí es correcta aplicando la fórmula del área de un triángulo:
Por lo tanto, el único modo de hallar el área es dividir los intervalos, de modo que dentro de cada uno la función no varíe su signo.
Emplea la siguiente aplicación para calcular el área de funciones con el eje OX dentro de un intervalo [a,b]. Si no especificas el intervalo, calcula únicamente las áreas de regiones cerradas.
|
|
Usa el símbolo ^ para las potencias |
Ejemplo 1
Calcular el área de la función 
,
el eje OX, y las rectas x = 1 y x = 4.
Ejemplo 2
Hallar el área de la función 
y el eje OX.
Debemos calcular los puntos de corte de la función con el eje OX.
Por tanto las raíces son: x = -2, x = 0, x = 1.
El área bajo la función f(x) es:
Ejemplo 3
Determina el valor de a con a > 0 y entero
para que el área de la región limitada por 
,
el eje OX, el eje OY y la recta x=a, sea igual a 21 u.a.
El área definida es:
Tenemos entonces que:
Resolvemos la ecuación, obteniendo a1 = -6.3218, a2 = 3.3218, a3 = 3.
Como a es positivo y entero, la solución válida es a = 3.
colaboradoras:
